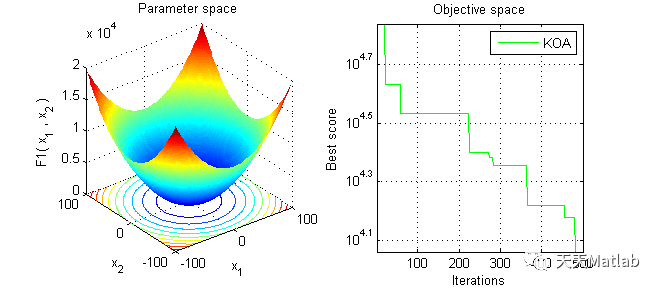
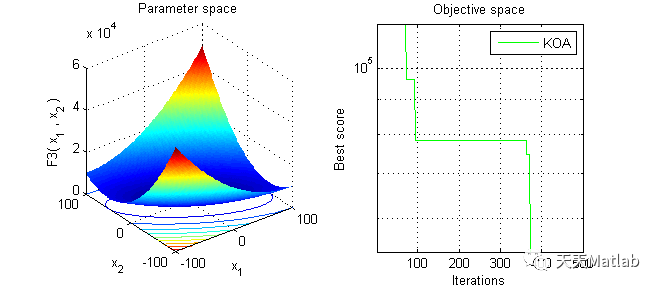
【智能优化算法】开普勒优化算法KOA附matlab代码

作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，

代码获取、论文复现及科研仿真合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击👇

智能优化算法 ? 神经网络预测 ? 雷达通信?? ? ?无线传感器 ? ? ?电力系统

信号处理 ? ? ? ? ? ?图像处理 ? ? ? ? ? 路径规划 ? 元胞自动机 ? ? ?无人机

智能优化算法是一种通过模拟自然界中的生物进化、群体行为或其他自然现象来解决复杂问题的方法。在这些算法中，开普勒优化算法（KOA）是一种基于天体运动原理的智能优化算法，它模拟了行星围绕太阳的运动规律，以解决优化问题。

KOA算法的流程包括以下几个步骤：

1. 初始化种群：首先，需要随机生成一组行星的初始位置和速度作为种群的初始解。这些行星的位置和速度将在算法的迭代过程中不断更新。

2. 计算适应度：对于每个行星的位置，需要计算其适应度值。适应度值是根据问题的特定目标函数计算得出的，用于衡量解的质量。

3. 更新速度和位置：根据行星的当前位置和速度，使用开普勒定律和万有引力公式来更新它们的速度和位置。这些更新将引导行星向更优解的方向移动。

4. 更新全局最优解：在每次迭代中，需要比较每个行星的适应度值与当前全局最优解的适应度值，并更新全局最优解。

5. 终止条件判断：在每次迭代后，需要判断是否满足终止条件。终止条件可以是达到最大迭代次数或找到满足特定要求的解。

6. 迭代更新：如果终止条件未满足，就回到第3步，继续更新行星的速度和位置，并更新全局最优解。

7. 输出结果：当算法达到终止条件时，输出最终的全局最优解作为算法的结果。

KOA算法的优点在于它能够在解空间中快速收敛到全局最优解，并且对于复杂的非线性优化问题具有较好的适应性。它也可以灵活地应用于各种不同类型的问题，例如函数优化、机器学习和组合优化等领域。

然而，KOA算法也存在一些挑战和限制。首先，算法的性能高度依赖于问题的特性和参数的选择。不同的问题可能需要不同的参数设置来获得最佳性能。此外，KOA算法对问题的初始解的选择也非常敏感，不同的初始解可能会导致不同的收敛速度和结果质量。

总之，开普勒优化算法是一种基于天体运动原理的智能优化算法，通过模拟行星围绕太阳的运动规律来解决优化问题。它具有快速收敛、适应性强等优点，但也需要合适的参数和初始解选择。随着智能优化算法的不断发展，KOA算法将在解决更多实际问题中发挥重要作用。

🎈 部分理论引用网络文献，若有侵权联系博主删除

🎁 ?关注我领取海量matlab电子书和数学建模资料

👇 ?私信完整代码、论文复现、期刊合作、论文辅导及科研仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合