优化算法之手推遗传算法（Genetic Algorithm）详细步骤图解

遗传算法是元启发式算法之一。 它有与达尔文理论（1859 年发表）的自然演化相似的机制。 如果你问我什么是元启发式算法，我们最好谈谈启发式算法的区别。

启发式和元启发式都是优化的主要子领域，它们都是用迭代方法寻找一组解的过程。启发式算法是一种局部搜索方法，它只能处理特定的问题，不能用于广义问题。而元启发式是一个全局搜索解决方案，该方法可以用于一般性问题，但是遗传算法在许多问题中还是被视为黑盒。

那么，遗传算法能做什么呢?和其他优化算法一样，它会根据目标函数、约束条件和初始解给我们一组解。

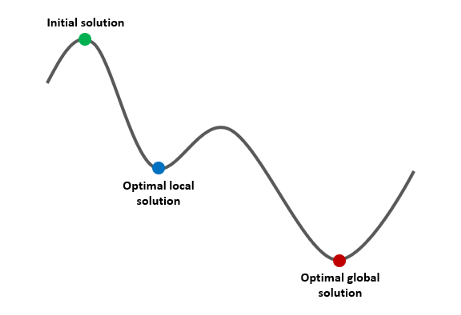
最优局部解与最优全局解

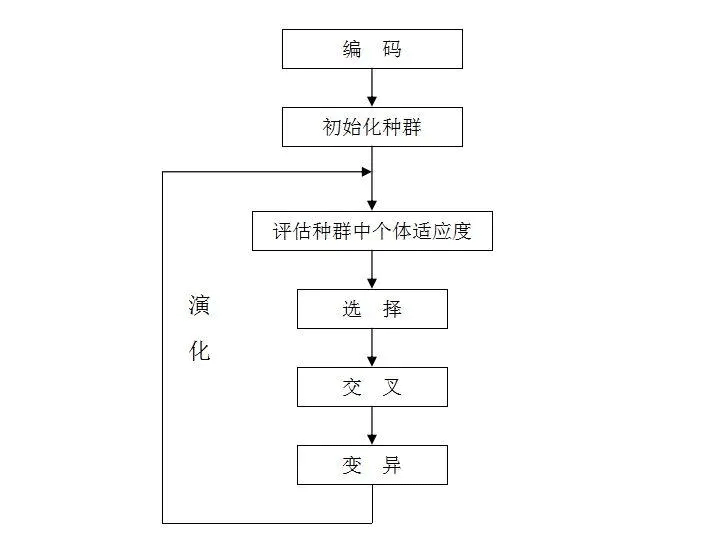
遗传算法有5个主要任务，直到找到最终的解决方案。它们如下。

• 初始化
• 适应度函数计算
• 选择
• 交叉
• 突变

我们将使用以下等式作为遗传算法的示例。 它有 5 个变量和约束，其中 X1、X2、X3、X4 和 X5 是非负整数且小于 10（0、1、2、4、5、6、7、8、9）。 使用遗传算法，我们将尝试找到 X1、X2、X3、X4 和 X5 的最优解。

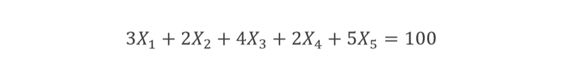
将上面的方程转化为目标函数。 遗传算法将尝试最小化以下函数以获得 X1、X2、X3、X4 和 X5 的解决方案。

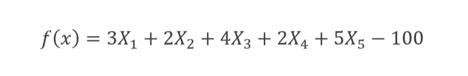
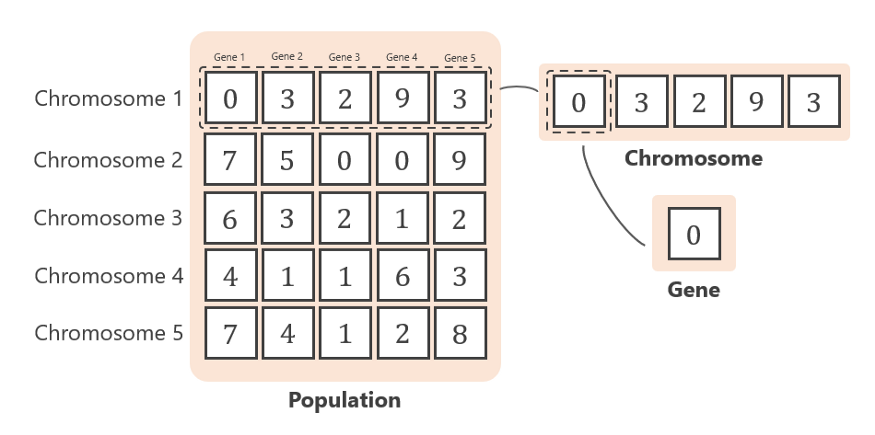
由于目标函数中有 5 个变量，因此染色体将由 5 个基因组成，如下所示。

在初始化时，确定每一代的染色体数。 在这种情况下，染色体的数量是 5。因此，每个染色体有 5 个基因，在整个种群中总共有 25 个基因。 使用 0 到 9 之间的随机数生成基因。

在算法中：一条染色体由几个基因组成。 一组染色体称为种群

下图是第一代的染色体。

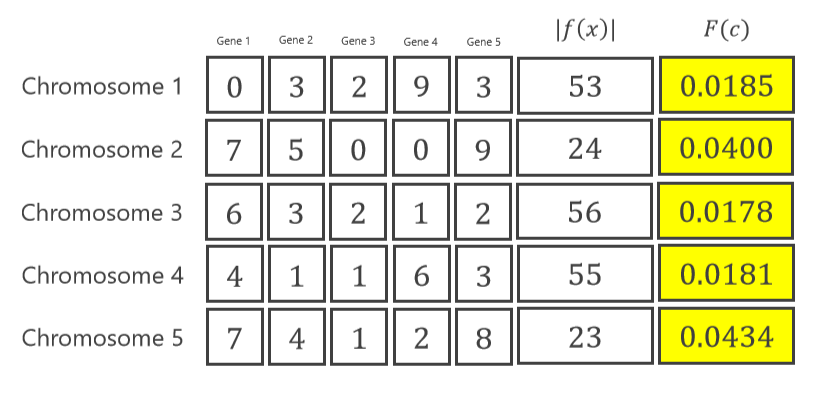
它也被称为评估。 在这一步中，评估先前初始化中的染色体。 对于上面示例，使用以下的计算方式。

这是第一代种群中的第一个染色体。

将 X1、X2、X3、X4 和 X5 代入目标函数，得到 53。

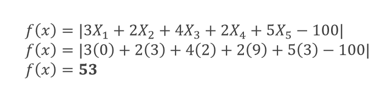
适应度函数是 1 除以误差，其中误差为 (1 + f(x))。

下面公式中加 1 是为了避免零问题

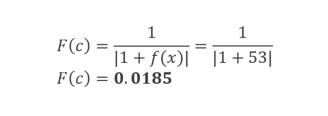
这些步骤也适用于其他染色体。

轮盘赌法是遗传算法中的一种随机选择方法。 这就像赌场里的轮盘赌。 它有一个固定点，并且轮子旋转直到轮子上的一个区域到达固定点的前面。

在遗传算法的背景下，具有较高适应度值的染色体将更有可能在轮盘赌中被选中。

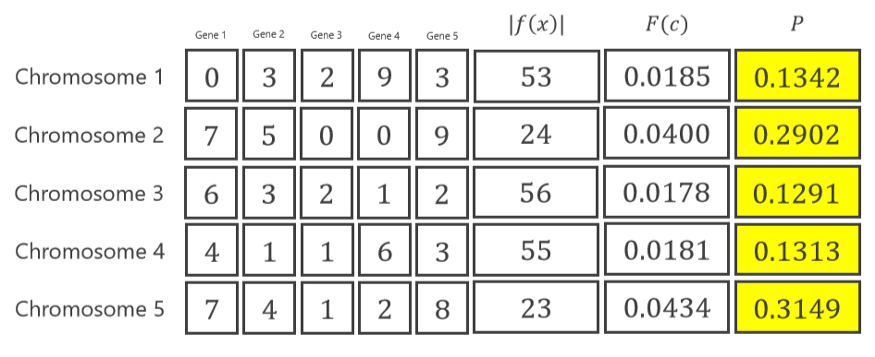
首先，计算 5 条染色体的总适应度值。

总计=.
总计=0.0185 + 0.0400 + 0.0178 + 0.0181 + 0.0434

然后，计算每个染色体的概率。 下图是第一条染色体概率的样本计算（P1=0.1342）。

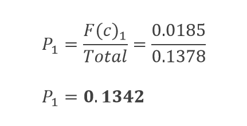
再次应用到所有的染色体：

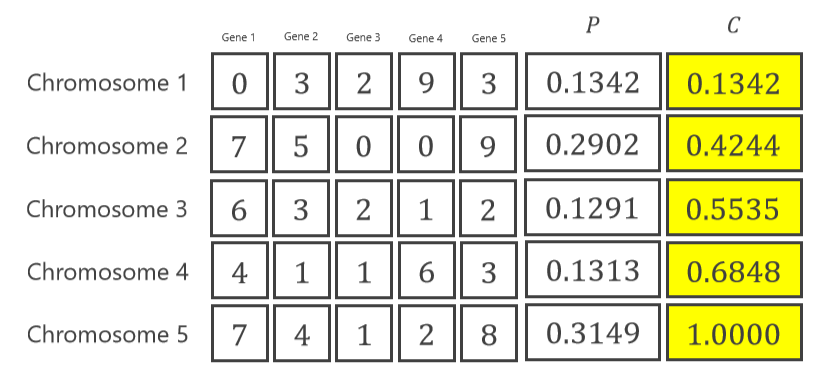
计算概率后，对于轮盘赌方法，需要计算其累积概率。

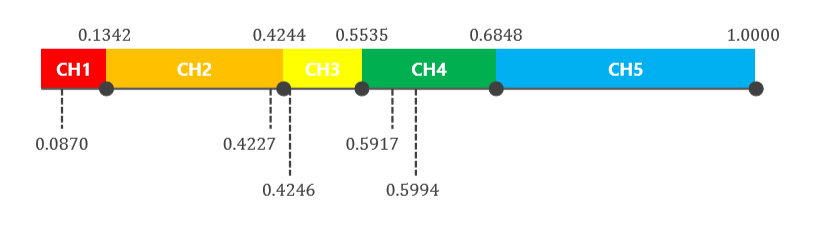
计算累积概率后，要使用轮盘进行选择，需要生成5个随机数Uniform(0,1)，这些随机数决定了从选择中剔除哪条染色体。

产生5个数字因为我们有5条染色体

下图就是挑选和消除染色体的方法。首先，根据累积概率排列染色体，所选择的染色体由随机数决定如下:

选择后的新染色体如下所示。

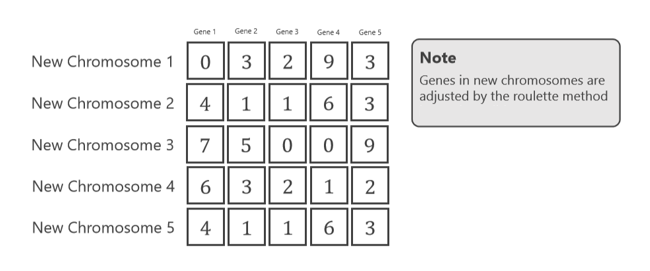
在生物学中，交叉是指生殖的一个术语。两条染色体被随机选择并通过数学运算进行匹配。在本例中使用单点交叉。

单点交叉意味着两个亲本的基因被一个交叉线交换

下图包含使用Uniform(0,1)生成的随机数。选择用于交叉的染色体数量是由交叉率(Pc)控制的，其中最小值为0，最大值为1。例如确定Pc=0.25，这意味着随机数目小于0.25的染色体将成为交叉中的亲本。

随机数对染色体。例如，R1对1号染色体，R2对2号染色体，以此类推

交叉的染色体是染色体1，染色体3和染色体5。这三条染色体的结合如下所示。

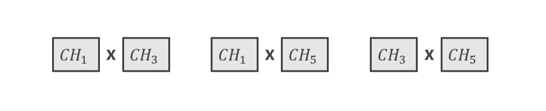
为了确定交叉线的位置，需要生成一个1到n之间的随机数，其中n是染色体- 1的长度。我们生成了1到4。

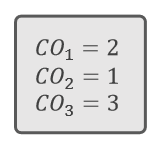
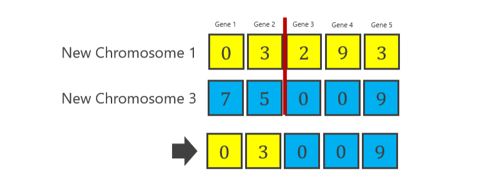
染色体1和染色体3之间的交叉(称为CO1)如下所示。

1号染色体和5号染色体之间的交叉(称为CO2)如下所示。

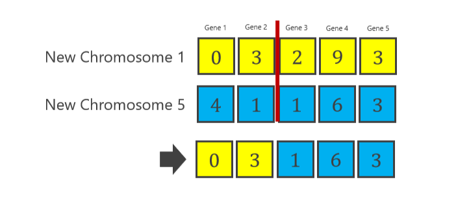
3号染色体和5号染色体(称为CO3)

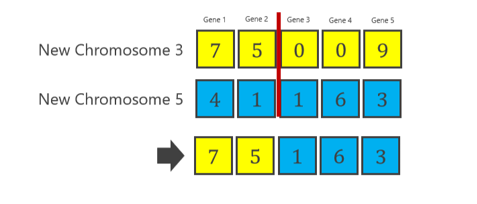
1号染色体和2号染色体来自新的2号染色体和4号染色体。他们没有被选中进行交叉。而染色体3、4和5来自前代的交叉。

下图就是与“染色体选择后使用交叉的结果”进行的对比。

突变是我们赋予任何基因新的价值的过程。在本例中使用随机突变，突变基因的数量由突变率决定( )。首先，计算一个种群中的基因数量。

基因总数=染色体 x 染色体中的基因数

接下来，发生突变的基因数量如下。

#突变的基因数=基因总数 x

因此，一个种群中的基因数量如下。

#genes=5 x 6
#genes=30

突变基因数(=0.1)

#genes mutation=30 x 0.1
#genes mutation=3

所以需要生成从1到30的随机数。随机数的结果是7、19和23。它们是突变基因的位置。接下来，对于每一个被选中的基因，生成一个从0到9的随机数来替换旧的值。

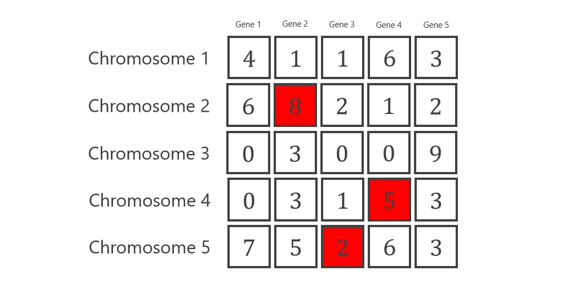
这些突变后的新染色体是第二代

对突变后的染色体进行评估。

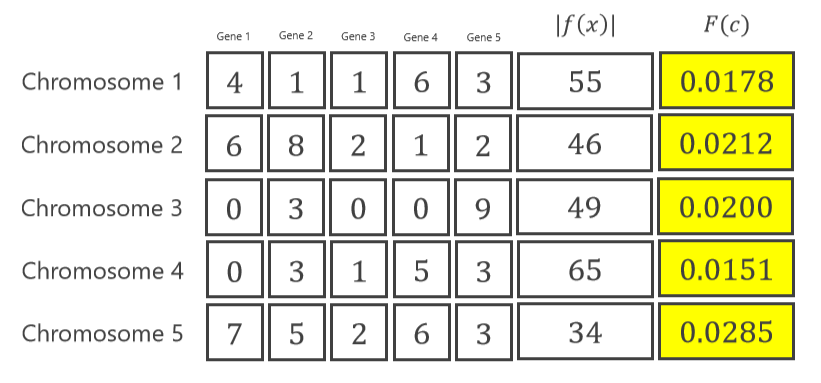
使用生成的新一代重复这个过程，就可以以获得X1、X2、X3、X4和X5的最佳解。经过几代后，得到的最佳染色体如下。

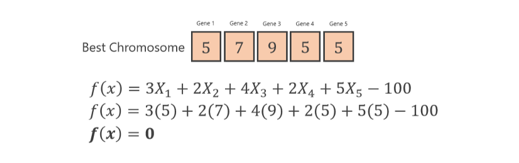
这个目标函数是有不同解的，所以我们这里只给出一个。如果需要添加限制条件，可以修改目标函数

下面的Jupyter Notebook是上面我们过程的代码实现：

https://gist.github.com/audhiaprilliant/f507d629a5322ca7f1ceaea027df0f6f

引用

[1]M. Fronita, R. Gernowo, V. Gunawan. 2017. Comparison of Genetic Algorithm and Hill Climbing for Shortest Path Optimization Mapping. The 2nd International Conference on Energy, Environment and Information System (ICENIS 2017). August 15th — 16th 2017. Semarang (ID). pp: 1–5.

[2]N. Arfandi, Faizah. 2013. Implementation of genetic algorithm for student placement process of community development program in Universitas Gadjah Mada. Journal of Computer Science and Information. 6(2): 70–75.

[3]T. Suratno, N. Rarasati, Z. Gusmanely. 2019. Optimization of genetic algorithm for implementation designing and modelling in academic scheduling. Eksakta: Berkala Ilmiah Bidang MIPA. 20(1): 17–24.

作者：Audhi Aprilliant